
算法学习之Java篇
一些需要记忆的内容
io模板
注意点:
①只要使用了PrintWriter、StringTokenizer、BufferedReader就必须try{ }catch( ){ },不然就会无法输出
②一定熟记printf的各种类型的输出符
③Scanner和PrintWriter等输入,输出一定要在使用后关闭
④一定要在声明数据时就初始化,这是java的特性对于基础数据类型而言就是赋初值;对于引用型数据类型 或 类 而言,就是在使用时一定要new
//常用包
import java.io.*;
import java.math.*;
import java.text.*;
import java.util.*;
public class Main {
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
public static void main(String args[]){
try{
String t1,t2;
t1 = cin.nextStr();
t2 = cin.nextStr();
solution1(t1,t2);
}
catch(Exception e){
cout.println(e.fillInStackTrace());
}finally {
cout.close();
}
}
//下面的solution方法写解题方案,具体情况视情况而定
static void solution1(String s, String t){
cout.printf("1:%s",s);
cout.printf("2:%s",t);
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//读取字符,nextToken()方法分割并单个读取字符
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();//读取下一个token里的数据
}
//读取一行数据
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
//读取一个整数
int nextInt(){
return Integer.parseInt(nextStr());
}
//读取一个浮点数
double nextDouble(){
return Double.parseDouble(nextStr());
}
//读取一个长整型
long nextlong(){
return Long.parseLong(nextStr());
}
//读取一个大整数【BigInteger包含在java.math包中】
BigInteger nextBig(){
return new BigInteger(String.valueOf(Integer.parseInt(nextStr())));
}
//后续还需要什么数据类型直接加函数就行了
//都是相同的道理:一个分装类对应一个基本数据类型
//上面的函数的返回类型最好是基础数据类型int,double,long等,当然也可以是包装类型但是性能没那么好
}printf输出符
字符串/字符
%s:字符串(char也可以输出)
%s:输出小写字母的字符串(char也可以输出)
%S:输出大写字母的字符串(char也可以输出)
%c:输出字符
整数
%d :有符号十进制整数
%o : 输出八进制整数
%x : 输出十六进制整数(eg:a、b等)
%X : 输出大写十六进制整数(eg:A、B等)
System.out.printf("%d %o %x %X", 10, 10, 10, 10);
// 输出 "10 12 a A"浮点数
%f:浮点数(包含float和double)默认保留到小数点后6位
%e : 输出科学计数法表示的浮点数(小写e)默认保留到小数点后6位
%E : 输出科学计数法表示的浮点数(大写E) 默认保留到小数点后6位
%.nf : 控制小数点后的位数,n为数字
System.out.printf("%.2f\n %e\n %E\n", 1500000.123441, 1500000.123441, 1500000.123441);
// 输出
1500000.123
1.500000e+06
1.500000E+06布尔值
%b : 输出布尔值
宽度和精度格式化
%n$ : 指定第n个参数
%m.n : 控制宽度和精度,m表示最小宽度,n表示小数点后的位数
System.out.printf("%2d%15.2f %s", 10, 3.1415926, "hello"); // 输出为: "10 3.14 hello" //即10和3.14中间隔断了(15-4)=11个单位【数字和小数点均占一位】 //也可选择用0来补齐这些空位 System.out.printf("%2d%015.2f %s", 10, 3.1415926, "hello"); //当然:这样就很奇怪。。 //输出为:"10000000000003.14 hello"
可用于时间格式的输出(十位补0):
//返回指定的时间样式的输出格式
System.out.printf("%02d:%02d:%02d\n",t/3600,t/60%60,t%60);宽度的定义:
可以在"%"和字母之间的数字表示最大场宽。
例如: %3d 表示输出3位整型数, 不够3位右对齐。
%9.2f 表示输出场宽为9的浮点数, 其中小数位为2, 整数位为6, 小数点占一位, 不够9位右对齐。
%8s 表示输出8个字符的字符串, 不够8个字符右对齐。
如果字符串的长度、或整型数位数超过说明的场宽, 将按其实际长度输出。
但对浮点数, 若整数部分位数超过了说明的整数位宽度, 将按实际整数位输出;
若小数部分位数超过了说明的小数位宽度, 则按说明的宽度以四舍五入输出。
对于整数和字符串来说,不存在精度问题。
对于浮点来说,所谓的精度是指小数位宽度。\n:换行符
java常用方法
限定小数点后位数【也遵从四舍五入】
可利用 String 的 format( , )方法:
第一个参数为匹配值:小数点后指定为多少位(eg:“%.2f” 代表保留小数点后2位)
第二个参数为 需要转换的值
示例:
n = 1.234567;
String s = String.format("%.2f", n);
cout.printf("%s",s);
//输出:1.23(转换为String就是对应的小数点后2位)
n = Double.parseDouble(s);
cout.printf("%f\n",n);
//输出:1.230000(因为double默认为小数点后6位)
//相当于对小数点某位后的数字起截断作用,
//也可指定位数
//如:保留小数点后三位
cout.printf("%.3f",m);
//输出:1.230除此之外,还可以用于转换进制(与printf输出格式一致):
用上面的格式化函数可以轻松实现数字的进制转换
--数字转换为八进制字符串
str = String.format("%o",23);
--数字转换为十六进制字符串
str = String.format("%x",23);
//大写十六进制字符串同理
str = String.format("%X",23)text下的SimpleDateFormat类及DecimalFormat类
获取毫秒数
Java Date类的getTime()方法返回自1970年1月1日GTM的00:00:00(由Date对象表示)以来的毫秒数。
所以可以用两个Date对象的差值来表示输入的两个时间相差多少毫秒
注意:以下为伪代码,仅用于说明原理
import java.util.Scanner;
//需要引入java.text包
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Date;
//返回指定的时间样式的输出格式:限定整数部分最多两位,不足两位用0来补齐
System.out.printf("%02d:%02d:%02d\n",t/3600,t/60%60,t%60);
long getMs() throws ParseException{
String line = in.nextLine();
//以空格为分隔符获取 开始时间 和 结束时间
String[] split = line.split(" ");
//时间解析的API SimpleDateFormat
SimpleDateFormat fmt = new SimpleDateFormat("HH:mm:ss");
//将字符串按照 指定时间格式fmt 来解析日期
Date t1 = fmt.parse(split[0]);
Date t2 = fmt.parse(split[1]);
//调用Date类的getTime()方法得到时间代表的毫秒数,故需要除以1000才表示秒数
return t2.getTime()/1000-t1.getTime()/1000;
}DecimalFormat四舍五入保留n位小数(不常用)
创建DecimalFormat类的对象
import java.text.DecimalFormat;//不要忘记导入包
//.后面的0的个数就是保留多少位小数
//DecimalFormat的格式控制见精确小数BigDecimal部分
DecimalFormat df = new DecimalFormat(".00");
double x = 8.055;
System.out.println(df.format(x));
//注意:这个地方涉及到一个陷阱!!!
//本来应该是8.06,但因为double型变量本身不准确,所以转换后结果却为:8.05
//所以我们才需要使用BigDecimal来精确计算机对于浮点数的精确程度valueof( )方法
参考:Java valueOf() 方法 | 菜鸟教程 (runoob.com)
public class Test{
public static void main(String args[]){
Integer x =Integer.valueOf(9);
Double c = Double.valueOf(5);
Float a = Float.valueOf("80");
Integer b = Integer.valueOf("444",16); // 使用 16 进制
System.out.println(x);
System.out.println(c);
System.out.println(a);
System.out.println(b);
}
}
//输出结果:
9
5.0
80.0
1092Math类相关方法
最大最小值max,min
Math.max(a,b)
Math.min(a,b)
求平方根sqrt/求a的b次方
Math.sqrt(a)
Math.pow(a,b)
注意:因为两个方法返回的都是double型数据,所以如果需要的类型是int,需要强转为int
开根号:Math.sqrt( y );
a的b次方:Math.pow( a,b ); //当将b设置为小于1的数时代表开多少次的根号
获取字符串/数组的长度
//数组长度:
int nums[] = {1,2,4,5,8};
int len = nums.length;
//字符串长度:
String a = "adsfdf";
int lens = a.length();Collections系列方法
collections的方法的对象都是 集合(eg:List< int > col、List< Integer > coll 等) ,不能是数组(基本数据类型),也不能是Integer(包装数据类型)
max、min
求最大最小值
示例:
// create link list object
List<Integer> list = new LinkedList<Integer>();
// populate the list
list.add(10);
list.add(20);
list.add(30);
list.add(40);
// printing the List
System.out.println("List: " + list);
// getting minimum value
// using min() method
int min = Collections.min(list);
// printing the min value
System.out.println("Minimum value is: " + min); equals
Collection<Integer> collection = new HashSet<>();
Collection<Integer> collection1 = new HashSet<>();
collection.add(5);
collection1.add(5);
collection1.add(8);
//will return true if both the collections are equal
boolean val=collection.equals(collection1);
System.out.println("Equals methods will return:"+val);Arrays类系列方法
Arrays的方法的对象可以是 集合(eg:List< int > col、List< Integer > coll 等) ,也可以是数组(基本数据类型),也不能是Integer(包装数据类型)
注意:Arrays的方法仅作用于一维数组,如果需要对二维数组进行操作,需要按照以下示例进行操作:
//用一维数组去填充二维数组中的每一个元素(即为一个一维数组)
static int a[][] = new int [101][101];
n = cin.nextInt();
m = cin.nextInt();
//a = new int[n+3][m+3];
int temp[] = new int[101];
Arrays.fill(temp,-1);
Arrays.fill(a,temp);
for(int i=0; i<n; i++){
for(int j=0; j<m; j++){
cout.printf("%d ",a[i][j]);
}
cout.printf("\n");
}
//当输入为:4 5时,
//输出的二维数组为:
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
//或者:
//使用a.clone( )函数
//当ten中的数值不固定,也不一定有规律时,
int[][] map=new int[4][5];
int[] ten={1,2,6,3,6,1,7};
for(int i=0;i<map.length;++i){
map[i] = ten.clone();
}sort排序
(1)普通排序:(默认将一个数列按照从小到大的顺序进行排序)
示例:
Arrays.sort(a);(2)对数组的部分进行排序
从fromIndex到toIndex-1的元素排序,注意:下标为toIndex的元素不参与排序
示例:
Arrays.sort(int[] a, int fromIndex, int toIndex)(3)构造比较器进行排序
Comparator 就是java.util里的一个第三方工具类,需要继承Comparator接口,所以在使用前要先实现myComparator(即自定义的比较器)类:
//方法定义:
public static void sort(T[] a,int fromIndex,int toIndex, Comparator c)
////第一种定义(有局限性,不推荐使用)
class myComparator implements Comparator{
//此处compare函数的类型、参数类型(但个数必须是两个)可以随意指定
public int compare(int a,int b){
if(a<b){return 1;}
else if(a>b){
return -1;
}else{return 0;}
}
//不指定开始和结束下标默认为全部都排
Arrays.sort(int[] a,2,3,new myComparator());
//但是返回int类型容易造成大数溢出,故可以考虑直接使用包装数据类型Integer,
//而不是使用以上传统的compare返回的基本数据类型int
////第二种定义(**推荐使用**)
Integer[] integers=new Integer[]{2,324,4,4,6,1};
Arrays.sort(integers, new Comparator<Integer>() {
public int compare(Integer o1, Integer o2) {
return o2 - o1;}
});
}
//在自定义类时:可以这样匿名构造
Arrays.sort(a, new Comparator<node>() {
@Override
public int compare(node x, node y) {
if(x.sum == y.sum) {
return x.sa - y.sa;
}
return x.sum - y.sum;//依据x>y来排序
}
} );
//对于数组进行从大到小的排序,则可以直接使用用java自带的函数Collections.reverseOrder( )
////第三种定义(***常用***)
public class text1
{
public static void main(String []args)
{
Integer[] integers=new Integer[]{2,324,4,4,6,1};
Arrays.sort(integers, Collections.reverseOrder());
for (Integer integer:integers)
{
System.out.print(integer+" ");
}
}
}fill填充
Arrays.fill(dp, 1);
将数组dp全部用1来填充
equals比较
toCharArray( )
说明:将字符串String转换为字符数组char[ ]
使用:
char s = new char[10]; String temp; temp = cin.nextStr(); s = temp.toCharArray(); cout.printf("%s ",s[1]);
char[ ]转String
使用:
char[] cha = {'s','g','h'}; String n = String.valueOf(cha);
获取毫秒数
Java Date类的getTime()方法返回自1970年1月1日GTM的00:00:00(由Date对象表示)以来的毫秒数。
所以可以用两个Date对象的差值来表示输入的两个时间相差多少毫秒
注意:以下为伪代码,仅用于说明原理
import java.util.Scanner;
//需要引入java.text包
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Date;
//返回指定的时间样式的输出格式
System.out.printf("%02d:%02d:%02d\n",t/3600,t/60%60,t%60);
long getMs() throws ParseException{
String line = in.nextLine();
//以空格为分隔符获取 开始时间 和 结束时间
String[] split = line.split(" ");
//时间解析的API SimpleDateFormat
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
//format.parse(split[0])解析字符串为日期
Date t1 = format.parse(split[0]);
Date t2 = format.parse(split[1])
//getTime()得到时间代表的毫秒数,故需要除以1000才表示秒数
return t2.getTime()/1000-t1.getTime()/1000;
}大数BigInteger
常用函数
BigInteger and(BigInteger val) 返回两个大整数的按位与的结果
BigInteger not() 返回当前大整数的非
BigInteger or(BigInteger val) 返回两个大整数的按位或
BigInteger divide(BigInteger val) 返回两个大整数的商
BigInteger multiply(BigInteger val) 返回两个大整数的积
BigInteger add(BigInteger val) 返回两个大整数的和
BigInteger subtract(BigInteger val)返回两个大整数相减的结果
double doubleValue() 返回大整数的double类型的值
int intValue() 返回大整数的整型值
float floatValue() 返回大整数的float类型的值
long longValue() 返回大整数的long型值
BigInteger abs() 返回大整数的绝对值
BigInteger gcd(BigInteger val) 返回大整数的最大公约数
BigInteger max(BigInteger val) 返回两个大整数的最大者
BigInteger min(BigInteger val) 返回两个大整数的最小者
BigInteger mod(BigInteger val) 用当前大整数对val求模
BigInteger negate() 返回当前大整数的相反数
BigInteger pow(int exponent) 返回当前大整数的exponent次方
BigInteger remainder(BigInteger val) 返回当前大整数除以val的余数
BigInteger leftShift(int n) 将当前大整数左移n位后返回
BigInteger rightShift(int n) 将当前大整数右移n位后返回
String toString() 将当前大整数转换成十进制的字符串形式
说明:JAVA大数BigInteger 用于进行较大数据的加减乘除运算
使用:需要引入:import java.math.BigInteger;
//加法
Scanner cinn = new Scanner(System.in); BigInteger a = cinn.nextBigInteger(); BigInteger b = cinn.nextBigInteger(); cout.println( a.add(b) );//减法
Scanner cinn = new Scanner(System.in); BigInteger a = cinn.nextBigInteger(); BigInteger b = cinn.nextBigInteger(); cout.println( a.subtract(b) );//乘法
Scanner cinn = new Scanner(System.in); BigInteger a = cinn.nextBigInteger(); BigInteger b = cinn.nextBigInteger(); cout.println( a.multiply(b) );//除法 //常常需要考虑余数问题,除数为0、被除数为0的问题
Scanner cinn = new Scanner(System.in); BigInteger a = cinn.nextBigInteger(); BigInteger b = cinn.nextBigInteger(); BigInteger c = a.divide(b);
精确小数BigDecimal
Java在 java.math包 中提供的API类BigDecimal,用来对超过16位有效位的数进行精确的运算。双精度浮点型变量double可以处理16位有效数。
一般情况下,对于那些不需要准确计算精度的数字:
我们可以直接使用Float和Double处理,但是Double.valueOf(String) 和Float.valueOf(String)会丢失精度。
所以开发中,如果我们需要精确计算的结果,则必须使用BigDecimal类来操作。
常见构造函数
BigDecimal(int)
创建一个具有参数所指定整数值的对象
BigDecimal(double)
创建一个具有参数所指定双精度值的对象
BigDecimal(long)
创建一个具有参数所指定长整数值的对象
BigDecimal(String)
创建一个具有参数所指定以字符串表示的数值的对象
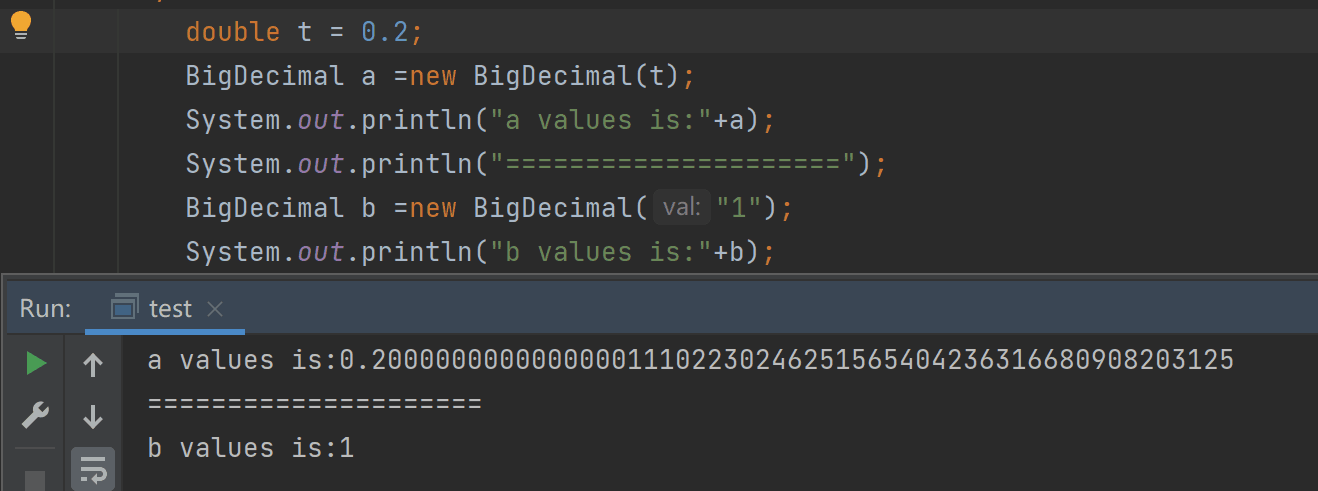
与其他构造方法相比,String 构造方法是完全可预知的:写入 newBigDecimal(“0.1”) 将创建一个 BigDecimal,它正好等于预期的 0.1。因此,比较而言, 通常建议优先使用String构造方法。
常用方法
add(BigDecimal)
BigDecimal对象中的值相加,返回BigDecimal对象
subtract(BigDecimal)
BigDecimal对象中的值相减,返回BigDecimal对象
multiply(BigDecimal)
BigDecimal对象中的值相乘,返回BigDecimal对象
divide(BigDecimal)
BigDecimal对象中的值相除,返回BigDecimal对象
toString()
将BigDecimal对象中的值转换成字符串
doubleValue()
将BigDecimal对象中的值转换成双精度数
floatValue()
将BigDecimal对象中的值转换成单精度数
longValue()
将BigDecimal对象中的值转换成长整数
intValue()
将BigDecimal对象中的值转换成整数
大小比较
bigdemical的compareTo方法
int a = bigdemical.compareTo(bigdemical2) //a = -1,表示bigdemical小于bigdemical2; //a = 0,表示bigdemical等于bigdemical2; //a = 1,表示bigdemical大于bigdemical2;
格式化
由于NumberFormat类的format()方法可以使用BigDecimal对象作为其参数,可以利用BigDecimal对超出16位有效数字的货币值,百分值,以及一般数值进行格式化控制。
NumberFormat currency = NumberFormat.getCurrencyInstance(); //建立货币格式化引用
NumberFormat percent = NumberFormat.getPercentInstance(); //建立百分比格式化引用
percent.setMaximumFractionDigits(3); //百分比小数点最多3位
BigDecimal loanAmount = new BigDecimal("15000.48"); //贷款金额
BigDecimal interestRate = new BigDecimal("0.008"); //利率
BigDecimal interest = loanAmount.multiply(interestRate); //相乘
System.out.println("贷款金额:\t" + currency.format(loanAmount));
System.out.println("利率:\t" + percent.format(interestRate));
System.out.println("利息:\t" + currency.format(interest));
//运行结果:
//贷款金额: ¥15,000.48 利率: 0.8% 利息: ¥120.00也可结合DecimalFormat类进行格式控制:
0 - 表示一个数字,如果该位置没有数字,则用 0 补充。
# - 表示一个数字,如果该位置没有数字,则不显示任何字符。
. - 用于分隔整数部分和小数部分。
, - 用于分隔整数部分的千位分隔符。
% - 用于将值乘以 100,并显示为百分数。import java.text.*;//不要忘记导入包
public class NumberFormat {
public static void main(String[] s){
System.out.println(formatToNumber(new BigDecimal("3.435")));
System.out.println(formatToNumber(new BigDecimal(0)));
System.out.println(formatToNumber(new BigDecimal("0.00")));
System.out.println(formatToNumber(new BigDecimal("0.001")));
System.out.println(formatToNumber(new BigDecimal("0.006")));
System.out.println(formatToNumber(new BigDecimal("0.206")));
}
/**
* @desc 1.0~1之间的BigDecimal小数,格式化后失去前面的0,则前面直接加上0。
* 2.传入的参数等于0,则直接返回字符串"0.00"
* 3.大于1的小数,直接格式化返回字符串
* @param obj传入的小数
* @return
*/
public static String formatToNumber(BigDecimal obj) {
//在此处传入的都是BigDecimal型变量,保证了准确性
DecimalFormat df = new DecimalFormat("#.00");
//等于0时:
if(obj.compareTo(BigDecimal.ZERO)==0) {
return "0.00";
}else if(obj.compareTo(BigDecimal.ZERO)>0&&obj.compareTo(new BigDecimal(1))<0){
//大于0小于1时:
return "0"+df.format(obj).toString();
}else {
//大于等于1时:
return df.format(obj).toString();
}
}
}转换回基本类型:
parse( )方法:本质上就是将返回的String转换为(基本数字类型)数字类Number

求最大公约数
用法:
①利用大数BigInteger中的方法 gcd( )
BigInteger x = scanner.nextBigInteger();//可以接收int类型 BigInteger y = scanner.nextBigInteger(); //也可以利用BigInteger.valueOf()将其他类型转换为BigInteger类型 BigInteger gcd = x.gcd(y); //BigInteger自带的求最大公约数的方法 a.gcd(b);②辗转相除法(自己写)【模板,记住即可】
public static int gcd(int a,int b){ if(b==0){ return a; } else{ return gcd(b,a%b); } }
求最小公倍数
首先要知道的结论:两个数的乘积等于这两个数的最大公约数与最小公倍数的积
所以:只需先利用上面一条结论求出最大公约数,然后用两个数的乘积/最大公约数 即可
分割函数split("分割符")【String才能用】
作用:用分割符来分割一行字符串内容的内容
与模板中的nextLine( )联合使用即可将一行有分割特征的字符串分割开来并存进数组中进行处理,如:
String s;
String str[ ];
str = cin.nextLine( ).split(" ");
//代表将一行字符串以“ ”为分隔符分割开来并分别存入str数组内
某字符串是否包含某个字符或字符串contains【String才能用】
虽然只有String才有该方法,但是StringBuffer和StringBuilder可以先通过toString方法先转换为String,再使用该方法。
//返回boolean类型的值:包含某一字符或者字符串时:返回true,否则返回false
StringBuilder sb = new StringBuilder("sss");
boolean s = (sb.toString()).contains("s");
//常常与charAt()函数配合使用(此时常常需要+""来转换为字符串,才能进行判断是否包含)
//因为charAt()返回值为char
int sum =0;
String str = 123+"";
for(int i=0; i<str.length(); i++){
if( "123456".contains( str.charAt(i)+"" ) ){ sum++; }
}拼接函数append("待拼接字符")【StringBuffer,StringBuilder才能用】
作用:在StringBuffer(或Stringbuilder)型字符串数据的后面拼接上一个字符串
(类似于String中的"+":String str = "abc"+"bcd";)
使用:
StringBuffer:
①构造
StringBuffer sb = new StringBuffer( );
//or
StringBuffer sb = new StringBuffer("abc")
②与String转换
String str = sb.toString( );
拼接(拼接对象为String):
sb.append("str");
更多StringBuffer方法见:Java StringBuffer 和 StringBuilder 类
截断函数substring()【Stringbuilder才能用】
示例:
import java.lang.*;
public class StringBuilderDemo {
public static void main(String[] args) {
StringBuilder str = new StringBuilder("admin");
System.out.println("string = " + str);
// prints substring from index 3
System.out.println("substring is = " + str.substring(3));
/* prints substring from index 1 to 4 excluding character
at 4th index */
System.out.println("substring is = " + str.substring(1, 4));}}
//
输出结果为:
string = admin
substring is = in
substring is = dmiString类常见函数
详见:java中String类的常用函数以及append()方法
数组填充函数
将dp[ ]数组全部填充上1
Arrays.fill(dp, 1);
需要明晰的知识
int 与char转换
重点在ascii码的运用上:
附大小写字母及基本字符的十进制ascii码对应表如下
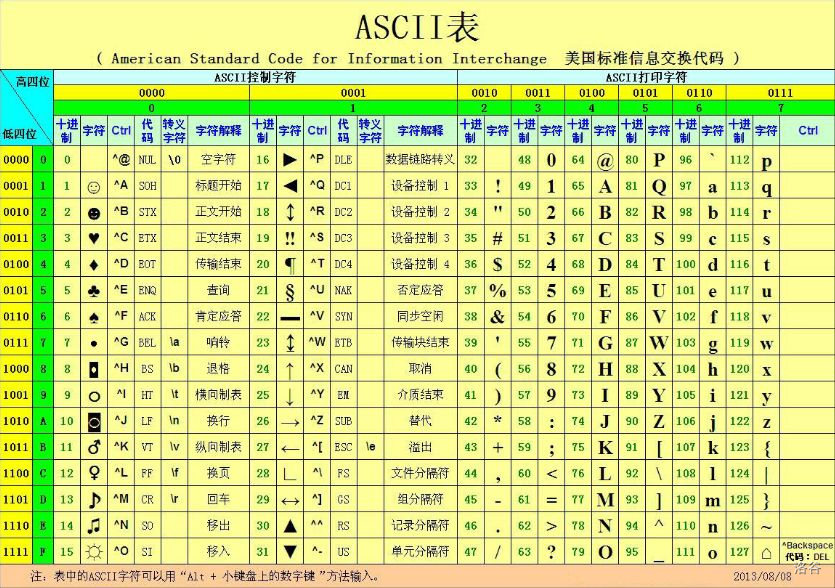
着重记忆:A--65 a--97
char 转 int
//a的值为:98-97 = 1 int a = 'b' - 'a'int 转 char
//若此时ind的值为0,则index=97,此时qw='a' int index = ind+97; char qw = (char)index;注意:在java中必须直接在一个 int型变量 前
直接加(char)进行强转,否则会失败
Parse()及相关方法用法
parse()是SimpleDateFomat里面的方法,java.lang包下为每一个基本数据类型提供了相对应的包装类。该类中最常用的方法是parseXXX( )方法,该方法可以将字符串转换成 相应的基本数据类型,但是前提是字符串的形式必须是相应的数据类型:
如:
//将字符串转换成Int型 String s = "123"; int b = Integer.parseInt(s);
valueOf()
用于如:Integer.valueOf() 是把 String类型 转化为Integer类型(注意:是Integer类型,而不是int类型,int类型是表示数字的简单类型,Integer类型是一个引用的复杂类型)
其他类型同理
数论基本知识
约数:又称因数,整数a除以整数b(b≠0)除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。如果一个整数同时是几个整数的约数/因子,称这个整数为它们的“公约数”;
最大公约数:公约数中最大的称为最大公约数
质数:又称素数,质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
质因数:也称(素因数或质因子),在数论里是指能整除给定正整数 的质数。
互质:除了1以外,两个没有其他共同质因子的正整数称为互质。
(1)两个不同的质数一定是互质数。
例如,2与7、13与19。
(2)一个质数,另一个不为它的倍数,这两个数为互质数。
例如,3与10、5与 26。
(3)1不是质数也不是合数,它和任何一个自然数(1本身除外)在一起都是互质数。如1和9908。
(4)相邻的两个自然数是互质数。如 15与 16。
(5)相邻的两个奇数是互质数。如 49与 51。
(6)较大数是质数的两个数是互质数。如97与88。
合数:非质数就是合数
自然数:非负整数。
因数:因数是指整数a除以整数b(b≠0) 的商正好是整数而没有余数,我们就说b是a的因数。
质数
判断一个数是否是质数
public static boolean isPrime1(int prime) { //for (int i = 2; i <= prime; i++) 全部遍历 /* 由于质数可以变成2个因子的乘,那么如果一个因子大于sqrt(x) 则另外一个小于sqrt(x),或者2个都是sqrt(x) 我们不采用Math.sqrt(x)函数,因为乘法比开根号效率要更高一些。 */ for (int i = 2; i * i <= prime; i++) if (prime % i == 0) return false; return true; }求范围内的质数
可以直接用上面的isPrimel( )函数依次进行判断输出,
但也可以考虑更快速的方法:埃式筛法
埃式筛法的思路:用已经筛选出来的素数去过滤所有能够被它整除的数。这些素数就像是筛子一样去过滤自然数,最后被筛剩下的数自然就是不能被前面素数整除的数,根据素数的定义,这些剩下的数也是素数。 如果需要多次判断素数,也可以用这个方法,每次用一个数组存储起来。
ArrayList<Integer> a =new ArrayList<>(); boolean[] b = new boolean[prime+1]; for (int i = 2; i <= prime; i++) { if (!b[i]){ a.add(i); //每次+i 相当于筛出所有当前素数的倍数出去 for (int j = i+i; j <= prime; j+=i) b[j] = true; } } return a;
最大公约数
//辗转相除法
public static int gcd(int a,int b){
if(b==0){ return a; }
else{
return gcd(b,a%b);
}
}最小公倍数
用两个数的乘积/最大公约数 即可
两个数互质(分解质因数来得到大数的约数个数)
2个数互质,说明其最大公约数为1
对应有一个算法:
实际上就是后面所讲的 “质因数分解结论”
详细可查看:分解质因数 - 知乎 (zhihu.com)
即 “分解质因数” :
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。 如30=2×3×5 。分解质因数 只针对合数 。
public static long countDivisor(long divisor){
long count = 1;
for (long i = 2; i*i <= divisor; i++) {
long numi = 0;
while (divisor % i == 0){
numi++;
divisor/=i;
}
count*=numi+1;
}if (divisor > 1)
count*=2;
return count;
}
//返回的结果就为该合数的约数个数java中常见数据类型的范围
int
【最高到2^10左右】
-2147483648~2147483647 ,占用4个字节(-2的31次方到2的31次方-1)
long
【最高到2^19左右】
-9223372036854774808~9223372036854774807 ,占用8个字节(-2的63次方到2的63次方-1)
float
3.402823e+38 ~ 1.401298e-45
(e+38表示是乘以10的38次方,同样,e-45表示乘以10的负45次方)占用4个字节
double
1.797693e+308~ 4.9000000e-324
占用8个字节
double型比float型存储范围更大,精度更高,所以通常的浮点型的数据在不声明的情况下都是double型的,如果要表示一个数据是float型的,可以在数据后面加上“F”。
java—Integer最大/小数
Integer.MAX_VALUE;
Integer.MIN_VALUE;
使用: int ma = Integer.MIN_VALUE;
集合
在使用时要注意以下问题:
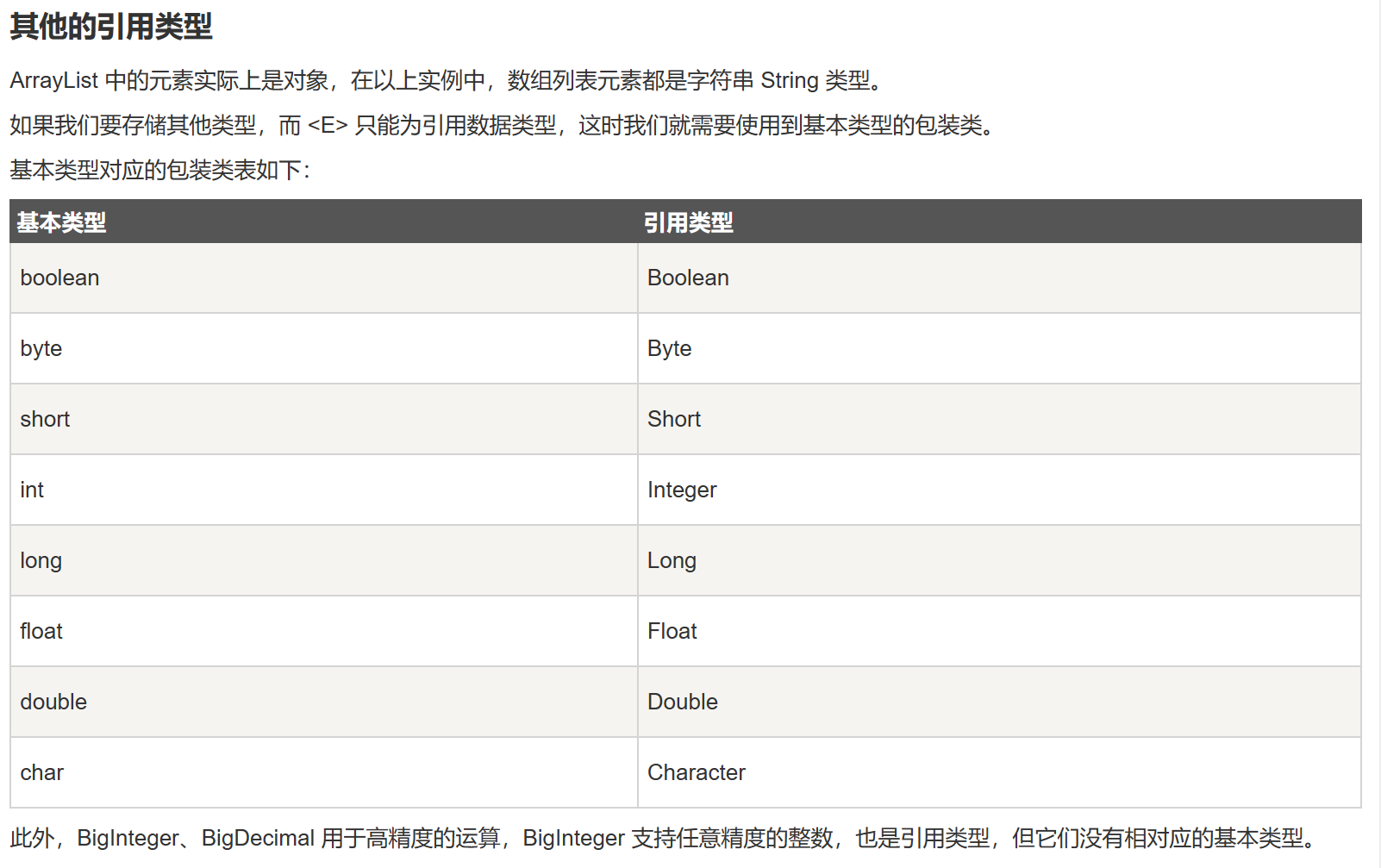
集合是java中提供的一种容器,可以用来存储多个数据。
集合和数组既然都是容器,但是:
数组的长度是固定的。集合的长度是可变的。
数组中存储的是同一类型的元素,可以存储基本数据类型值。集合存储的都是对象。而且对象的类型可以不一致。在开发中一般当对象多的时候,使用集合进行存储。
这些接口和类在java.util包中,因为类型很丰富,因此我们通常称为集合框架集
集合主要分为两大系列:Collection和Map:
Collection 表示一组对象,Map 表示一组映射关系或键值对。
Collection
Collection 层次结构中的根接口。Collection 表示一组对象,这些对象也称为 collection 的元素。
一些 collection 允许有重复的元素,而另一些则不允许;一些 collection 是有序的,而另一些则是无序的。
JDK 不提供此接口的任何直接实现:它提供更具体的子接口(如 Set 和 List、Queue)实现
List:有序的 collection(也称为序列)。此接口的用户可以对列表中每个元素的插入位置进行精确地控制。用户可以根据元素的整数索引(在列表中的位置)访问元素,并搜索列表中的元素。
Queue:队列通常(但并非一定)以 FIFO(先进先出)的方式排序各个元素。不过优先级队列和 LIFO 队列(或堆栈)例外,前者根据提供的比较器或元素的自然顺序对元素进行排序,后者按 LIFO(后进先出)的方式对元素进行排序。
Set:一个不包含重复元素的 collection。更确切地讲,set 不包含满足 e1.equals(e2) 的元素对 e1 和 e2,并且最多包含一个 null 元素。正如其名称所暗示的,此接口模仿了数学上的 set 抽象。
更多的:SortedSet进一步提供关于元素的总体排序 的 Set。这些元素使用其自然顺序进行排序,或者根据通常在创建有序 set 时提供的 Comparator进行排序。该 set 的迭代器将按元素升序遍历 set。提供了一些附加的操作来利用这种排序。
Map
Map:将键映射到值(key,value)的对象。
一个映射不能包含重复的键;每个键最多只能映射到一个值。 Map 接口提供三种collection 视图,允许以键集、值集或键-值映射关系集的形式查看某个映射的内容。映射顺序 定义为迭代器在映射的 collection 视图上返回其元素的顺序。某些映射实现可明确保证其顺序,如 TreeMap 类;另一些映射实现则不保证顺序,如 HashMap 类。
SortedMap进一步提供关于键的总体排序 的 Map。该映射是根据其键的自然顺序进行排序的,或者根据通常在创建有序映射时提供的 Comparator 进行排序。
单列集合(List和Set)通用的方法
附带一个单列集合的方法总结:
Java ArrayList | 菜鸟教程 (runoob.com)
1、添加元素
(1)add(E obj):添加元素对象到当前集合中
【还有指定下标插入的形式:add(int index, E element)】
(2)addAll(Collection<? extends E> other):添加other集合中的所有元素对象到当前集合中,即this = this ∪ other
2、删除元素
(1) boolean remove(Object obj) :从当前集合中删除第一个找到的与obj对象equals返回true的元素。
【还有另外一种形式:remove(int index):删除对应下标的元素,下标从0开始】
(2)boolean removeAll(Collection<?> coll):从当前集合中删除所有与coll集合中相同的元素。即this = this - this ∩ coll
3、判断元素
(1)boolean isEmpty():判断当前集合是否为空集合。
【不存在任何元素返回true; 存在元素返回false】
(2)boolean contains(Object obj):用于判断元素是否在动态数组中。
【如果指定的元素存在于动态数组中,则返回 true
如果指定的元素不存在于动态数组中,则返回 false】
(3)boolean containsAll(Collection<?> c):判断c集合中的元素是否在当前集合中都存在。即c集合是否是当前集合的“子集”。
【如果动态数组中包含的集合中的所有元素,则返回 true。
如果 arraylist 中存在的元素与指定 c中的元素不兼容,则抛出 ClassCastException。
如果 c中包含 null 元素,并且 arraylist 中不允许 null值,则抛出 NullPointerException 异常。】
4、查询
(1)int size():获取当前集合中实际存储的元素个数
(2)Object[] toArray():返回包含当前集合中所有元素的数组
【如果参数 T[] arr 作为参数传入到方法,则返回 T 类型的数组,例如:
ArrayList<String> sites = new ArrayList<>(); String[] arr = new String[sites.size()]; sites.toArray(arr);//则将集合转换后直接返回到arr中如果未传入参数,则返回 Object 类型的数组。】
5、交集
(1)boolean retainAll(Collection<?> coll):当前集合仅保留与c集合中的元素相同的元素,即当前集合中仅保留两个集合的交集,即this = this ∩ coll;
ArrayList<String> sites = new ArrayList<>(); sites.add("Google"); sites.add("Runoob"); sites.add("Taobao"); // 创建另一个动态数组 ArrayList<String> sites2 = new ArrayList<>(); // 往动态数组中添加元素 sites2.add("Wiki"); sites2.add("Runoob"); sites2.add("Google"); sites.retainAll(sites2); System.out.println("保留的元素: " + sites); //输出为: 保留的元素: [Google, Runoob]增强for(简洁遍历)
for(元素的数据类型 变量 : Collection集合or数组){ //写操作代码 } //示例: public class NBForDemo1 { public static void main(String[] args) { int[] arr = {3,5,6,87}; //使用增强for遍历数组 for(int a : arr){//a代表数组中的每个元素 System.out.println(a); } } } //对于集合而言,类型直接声明为Object即可: ArrayList<Integer> a = new ArrayList<Integer>(); for(Object i: x){ cout.printf("%d ",i); }
continue特殊用法
指定跳转的层:
//则每次运行continue语句就跳转到外层的循环语句
a: for(int i = 2019, n= 2019; true; n = i +=2019 ){
do {
if ((n & 1) == 0)
continue a;
} while ((n /= 10) > 0);
System.out.println(i);
break;
}判定每一位是否都为奇数
思想是 判定每一位与1的&之后的结果, 这是因为 只要是奇数二进制的最后一位必定是1,所以 ( 最后一位 & 1 ) == 0 证明当前数为奇数, 否则为偶数.
static boolean jug(int n){
boolean flag = false;
if((n & 1)==1){ flag =true; }
return flag;
}闰年和闰月
平年有365天,闰年有366天
1、3、5、7、8、10、12这七个月份每月都是31天。
4、6、9、11这四个月份每月都是30天。
2月要看是平年还是闰年,平年是28天, 闰年是29天。
年数判断是否为闰年:
年数 能被4整除 且 不能被100整除 的为闰年
年数 能被400整除 的是闰年
AcWing
概念性内容
二分模板
有两个模板:判断左侧还是判断右侧【两个模板通常选一个即可】
根据实际check( )来判断:即先判断a[mid]与待查找值k的大小关系
对于递增 的a[ ]有:
(模板Ⅰ)(mid初值= l+r >>1)若a[mid]>=k,则说明k存在于a[mid]左侧(更小的一侧),则赋值r=mid,反之赋值l=mid+1。
(模板Ⅱ)(mid初值= (l+r+1) >>1)若a[mid]<=k,则说明k存在于a[mid]右侧(更大的一侧),则赋值l=mid,反之赋值r=mid-1。
注意:当结束一次二分后,均有l=r,故后续无论使用哪个作为下标来使用都无所谓
模板Ⅰ的最终查找结果 l 和 r 是最左边的待查找值的下标
而模板Ⅱ的最终查找结果 l 和 r 是最右边的待查找值的下标
前缀和、差分(前缀和的逆运算)
对于前缀和而言:即求[l,r]下标内数组的和,先构造前n项和数组Sn即可,再由S[r] - S[l-1]即可得到
一定要注意前缀和、差分之间的关系,不然差分就不好理解。
本质上:对差分数组中的某一个b[l]进行常数加减,便能达到对l之后所有的a[ ](即:a[l],a[l+1],....a[n-1],a[n])都进行常数加减的作用。所以才需要再对b[r+1]进行相反的加减常数工作,这样才能对r+1之后所有的a[ ](即a[r+1],....a[n-1],a[n])进行相反的常数加减以达到“打补丁”的作用
而对于差分而言:核心就是需要构造出差分数组b[ ],而b[ ]的前缀和实际就是我们需要进行处理操作的普通数组a[ ],差分的目的也在于通过对差分数组b[ ]进行加减常数c从而达到对a[ ]进行加减常数c。构造差分数组b[ ]以及通过对b[ ]加减常数c从而达到对a[ ]加减c 均 通过公式:
①b[l] = b[l] + c
②b[r+1] = b[r+1] - c 来达成。
注意:构造差分数组b[]时,进行一个i的循环:l和r均等于i,常数c等于a[i]即可
离散存储
为什么用离散存储?
答:当数据的值域范围很广,但真正用到的数据却很少时,将离散的需要用到的值,稠密地放到同一个数组中,便于操作。
并查集
本质就是用构建树的方式来合并元素形成集合,将第一个在集合中的元素指定为自己的祖宗结点,而其他需要加入到该祖宗结点的元素想要合并到该祖宗结点所在的集合中只需要 指定该元素的祖宗结点为该祖宗结点 即可
按插入顺序排序的链表
问题针对对象:需要对按照先后顺序进行插入或删除值的链表
思路:利用两个数组:e[ ]、en[ ],分别存储 链表内每一顺序的值、链表内每一顺序值的下标
注意:此时的下标假设为idx,则idx表示的既是 “按照顺序插入” 又是 “链表的下标”
KMP字符串
AcWing 831. KMP字符串 —— 深入浅出 next 数组 - AcWing
关键点在于先要将NEXT[ ]数组的值找到,这个地方的NEXT数组中的值是字串p的最佳位置下标,求法是:
判断 j是否回退到 -1 、 p[ i ] == p[ j + 1 ] 是否成立 来决定当前子串和子串自身的下一个字符是否匹配上(即当前主串字符p[i]是否等于自身的下一个字符p[j+1]),不是匹配的就通过 j =NEXT[j] 来回退到该回退的位置上,直到匹配或者 j 回退到 -1,是匹配( p[ i ] == p[ j + 1 ])的就 j++ 并且令 NEXT[ i ] = j
在针对 真正的主串s 和 子串p 进行匹配的过程实际上是通过 判断 j是否回退到 -1 、 s[ i ] == p[ j + 1 ] 是否成立 来决定当前主串和子串的下一个字符是否匹配上(即当前主串字符s[i]是否等于子串的下一个字符p[j+1]),不是匹配的就通过 j =NEXT[j] 来回退到该回退的位置上,直到匹配或者 j 回退到 -1,是匹配( s[ i ] == p[ j + 1 ])的就 j++ (若要求求所有的匹配则 再令 j =NEXT[ j ] 即可 )
next 数组的含义就是当 j + 1 位失配时,j 应该回退到的位置
求解 next 数组的过程其实就是模式串 pattern 进行自我匹配的过程。
贪心
基本定义:每次查找当前局部的最佳解,不考虑其他的。(只考虑眼前情况)
由于每次只是求出的局部的最优解,所以就注定是鼠目寸光的,
但是如果想要放在全局来解决问题,那就似乎只能通过暴力枚举来凑出方案,明显复杂度过高。有太多种可能的情况了,枚举它们的时间是不可承受的。
动态规划
【如果一个奇葩国家的钞票面额分别是1、5、11,假设我们需要求凑出15的最少钞票数目】
w=15时,我们如果取11,接下来就面对w=4的情况;如果取5,则接下来面对w=10的情况。我们发现这些问题都有相同的形式:“给定w,凑出w所用的最少钞票是多少张?”接下来,我们用f(n)来表示“凑出n所需的最少钞票数量”。
那么,如果我们取了11,最后的代价(用掉的钞票总数)是多少呢?
明显:cost = f(4)+1 = 4+1 = 5 它的意义是:利用11来凑出15,付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。 依次类推,马上可以知道:如果我们用5来凑出15,cost就是 f(10)+1 = 2+1=3
那么,现在w=15的时候,我们该取那种钞票呢?当然是各种方案中,cost值最低的那一个:
--取11: cost = f(4)+1 = 4+1 = 5
--取5:cost = f(10)+1 = 2+1 = 3
--取1:cost = f(14)+1 = 4+1 = 5
故我们需要引入dp来进行解决问题,它与暴力的区别在哪里?我们的暴力枚举了“所有的纸币数额“,然而这属于冗余信息。我们要的是答案,根本不关心这个答案是怎么凑出来的。譬如,要求出f(15)【即15元钱最少需要多少张纸币才能凑出来】,只需要知道f(14),f(10),f(4)的值。其他信息并不需要。我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n).
取决于问题的性质:求出f(n),只需要知道几个更小的f(c)。我们将求解f(c)称作求解f(n)的“子问题”。
这就是DP(即:动态规划,dynamic programming).
将一个问题拆成几个子问题,分别求解这些子问题,即可推断出大问题的解。
质因数分解结论
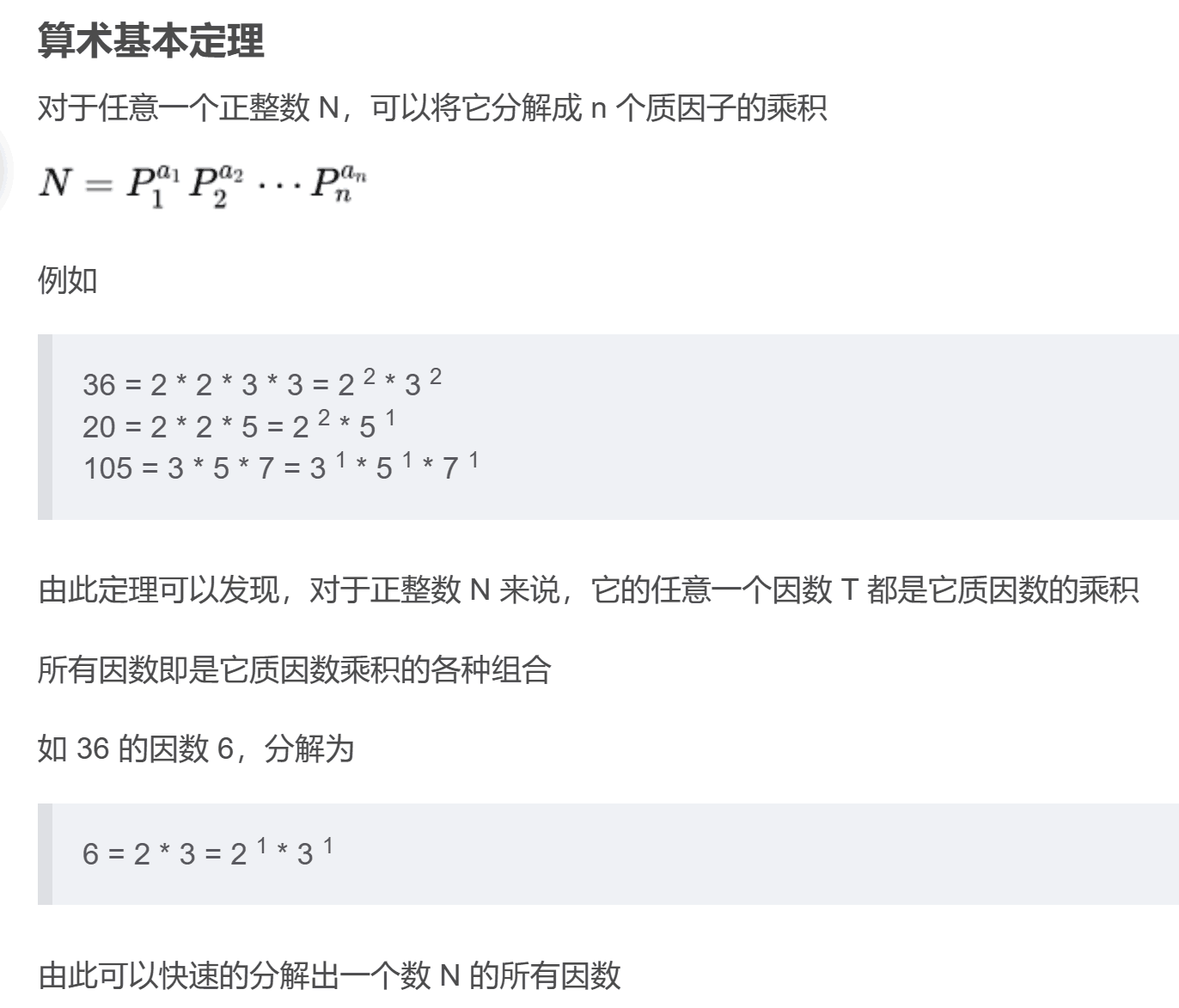
上面的基本结论可以得出快速分解出一个数的所有可能的因数的方法:
如:36的所有因数(除1和它本身外)就是2和3的所有排列组合后的结果,即6
同时,就可以推出该结论(得到某数的因数的个数):

从而:我们也可以得出一个结论,就是所有的数都可以被分解质因数为:2,3,5,7这四个数字的 0-n 次方(即指数可以为0-n) 之和。
且由第二个结论可知:因数个数为(各指数+1)之积
题记
题记【二进制中1的个数】(2022.12.6)
注意:
Java中的位运算符:
首先要有一个概念:计算机中使用的不是原码,而是补码。
故:正数负数都是使用的补码存储的;
而 正数因为补码等于原码所以也就是源码,负数的补码则等于(除开第一个符号位)所有位取反再加1的结果。
>>表示右移,如果 该数为正,则高位补0,若为负数,则高位补1;
>>>表示无符号右移,也叫逻辑右移,即 若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0。
所以如果 碰到有负数的情况,需要使用逻辑右移>>>来保证搜索1的个数
另外:还常用>>来表示对一个数(无论正负)除以2的操作【碰到有小数向下求】
同理,<<则表示对一个数(无论正负)进行乘以2的操作。
具体可见下列对于-2中1的计1(虽然很没有意义,但是原理解释清楚了):
public class test{ private static PrintWriter cout = new PrintWriter(System.out); static int intSize; public static void main(String args[]){ try{ int a = -2; intSize = Integer.SIZE; System.out.printf("一个int型数据所占位数为:%d\n",intSize); sol(a); //-2 的原码:1010 //-2 的补码:1110 }catch(Exception e){ cout.println("错误"); }finally{ cout.close(); } } static void sol(int t){ int count = 0; boolean f = true; while(f){ count+=t&1; t=t>>>1; if(t==0) f=false; } cout.printf("该数字有 %d 个1",intSize-count); } }
好了,现在正式进入这道题的部分,实际上就是一个x&1来统计x当前位(从最低位开始)是否为1,再x>>1将其右移以检查下一位。
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
public static void main(String args[]){
try{
int s;
s = cin.nextInt();
for(int i=0; i<s; i++){
int q = cin.nextInt();
sol(q);
if(i!=s-1){cout.printf("%s"," ");}
}
}catch(Exception e){
cout.println("错误");
}finally{
cout.close();
}
}
static void sol(int t){
int count = 0;
boolean f = true;
while(f){
count+=t&1;
t=t>>1;
if(t==0) f=false;
}
cout.printf("%d",count);
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st == null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
Double nextDouble(){
return Double.parseDouble(nextStr());
}
}题记【 数的范围(二分查找)】(2022.12.9)
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int a[]= new int[100000+10];
static int b[]= new int[10000+10];
static int n,q;
public static void main(String args[]){
try{
n = cin.nextInt();
q = cin.nextInt();
for(int i=0; i<n; i++){
a[i] = cin.nextInt();
}
for(int i=0; i<q; i++){
b[i] = cin.nextInt();
}
for(int i=0; i<q; i++){
//cout.printf("%d\n",b[i]);
sol(i);
}
}catch(Exception e){
cout.println("错误");
}finally{
cout.close();
}
}
//待查找的数是b[rs]
static void sol(int rs){
int l=0;
int r=n-1;
while(l<r){
int mid = (l+r) >>1;
if(a[mid] >= b[rs]){ r=mid; }
else{ l=mid+1; }
}
//cout.printf("%d %d\n",a[l],b[rs]);//测试使用
if(a[l]!=b[rs]){cout.printf("%d %d\n",-1,-1);}
else{
int left = l;
l= 0;
r= n-1;
while(l<r){//遍历完所有值时l=r
int mid= (l+r+1)>>1;
if(a[mid] <= b[rs]){ l=mid; }
else{ r=mid-1; }
}
cout.printf("%d %d\n",left,l);
}
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
Double nextDouble(){
return Double.parseDouble(nextStr());
}
}import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static final int N = 100000+10;
static int a[]= new int[N];
static int s[]= new int[N];
static int m,n;
static int l,r;
public static void main(String args[]){
try{
n = cin.nextInt();
m = cin.nextInt();
for(int i=1; i<=n; i++){
a[i] = cin.nextInt();
}
for(int i=1; i<=n; i++){
s[i]=s[i-1]+a[i];
}
for(int i=0; i<m; i++){
l = cin.nextInt();
r = cin.nextInt();
sol(l,r);
}
}catch(Exception e){
cout.println("错误");
}finally{
cout.close();
}
}
static void sol(int l,int r){
int sum = 0;
sum = s[r]-s[l-1];
cout.printf("%d\n",sum);
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
Double nextDouble(){
return Double.parseDouble(nextStr());
}
}题记【差分】(2022.12.10)
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int N = 100010;
static int a[] = new int[N];
static int b[] = new int[N];
static int n,m;
public static void main(String args[]){
try{
int l=0;
int r=0;
int c=0;
n= cin.nextInt();
m= cin.nextInt();
for(int i=1; i<=n; i++){
a[i]= cin.nextInt();
}
//由原数组进行自插入操作以 获取差分数组:这个步骤需要记忆
for(int i=1; i<=n; i++){
insert(i,i,a[i]);
}
//对差分数组进行题目要求的加减操作
for(int i=0; i<m; i++){
l= cin.nextInt();
r= cin.nextInt();
c= cin.nextInt();
sol(l,r,c);
}
//将差分数组自加 变为自己的前n项和(即重新获得原数组)
for(int i=1; i<=n; i++){
b[i]+=b[i-1];
}
//输出进行题目要求的操作后的原数组
for(int i=1; i<=n; i++){
cout.printf("%d ",b[i]);
}
}catch(Exception e){
cout.println("错误");
}finally{
cout.close();
}
}
static void sol(int l, int r, int c){
insert(l,r,c);
}
//理解记忆就会很简单(看总结)
static void insert(int l, int r, int c){
b[l]+=c;
b[r+1]-=c;
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
Double nextDouble(){
return Double.parseDouble(nextStr());
}
}
题记【区间和】(2022.12.14)
另外可以参考一个写的比较好的题解:区间和代码详解
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int N = 300010;
static int a[] = new int[N];
static int s[] = new int[N];
static int n,m;
public static void main(String args[]){
List<Integer> alls = new ArrayList<>();
List<Pairs> add = new ArrayList<>();
List<Pairs> query = new ArrayList<>();
try{
n = cin.nextInt();
m = cin.nextInt();
for(int i=0; i<n; i++){
int x= cin.nextInt();
int c= cin.nextInt();
add.add(new Pairs(x,c));
alls.add(x);
}
for(int i=0; i<m; i++){
int l = cin.nextInt();
int r = cin.nextInt();
query.add(new Pairs(l,r));
alls.add(l);
alls.add(r);
}
Collections.sort(alls);
int unique = unique(alls);
alls = alls.subList(0,unique);
for(Pairs item:add){
int index = find(item.first,alls);
a[index]+= item.second;
}
for(int i=1; i<=alls.size(); i++) s[i]=s[i-1]+a[i];
for(Pairs item:query ){
int l = find(item.first,alls);
int r = find(item.second,alls);
cout.printf("%d\n",s[r]-s[l-1]);
}
}catch(Exception e){
}finally{
cout.close();
}
}
static int unique(List<Integer> list){
int j =0;
for(int i=0; i<list.size(); i++){
if( i==0 || list.get(i)!=list.get(i-1) ){
list.set(j,list.get(i));
j++;
}
}
return j;
}
static int find(int x, List<Integer> list){
int l= 0;
int r= list.size()-1;
while(l<r){
int mid = l+r >>1;
if(list.get(mid)>=x){ r=mid; }
else{
l=mid+1;
}
}
return l+1;
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
Integer nextInt(){
return Integer.parseInt(nextStr());
}
}
class Pairs{
public int first;
public int second;
public Pairs(int a,int b){
this.first = a;
this.second = b;
}
}题记【并查集】(2023.2.22)
可结合这篇解析来深入理解并查集:AcWing 836. 合并集合解析
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int n,m;
static int q[] = new int[100000+10];
static int w;
public static void main(String args[]){
try{
w=0;
n= cin.nextInt();
for(int i=0; i<n; i++){ q[i+1] = i+1;}
m = cin.nextInt();
for(int i= 0; i<m; i++){
String traget;
traget = cin.nextStr();
int a,b;
if( traget.equals("M") ){
a = cin.nextInt();
b = cin.nextInt();
//合并操作:寻找a元素所在集合的代表元素(祖宗结点)
//并设置其为b所在集合的代表元素(祖宗结点)
//(指定其祖宗结点为另一结点的祖宗结点 就代表 完成一次插入)
q[find(a)] = find(b);
}
else{
a = cin.nextInt();
b = cin.nextInt();
if(jug(a,b)){cout.println("Yes");}
else{cout.println("No");}
}
}
}catch(Exception e){
cout.println("error");
}finally{
cout.close();
}
}
//find函数是关键,用于查找祖宗结点(或可说成寻找代表元素)
static int find(int i){
if( q[i] != i){ q[i] = find(q[i]); }
//因为初始情况下,q[i]=i,所以刚开始自己就是自己的祖宗结点
return q[i];
}
static boolean jug(int a,int b){
if( find(a) == find(b) ){return true;}
else{ return false; }
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【按照顺序插入的链表】(2023.2.23)
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int M;
static int e[] = new int[100000+10];
static int en[] = new int[100000+10];
static int head,idx;
public static void main(String arg[]){
try{
head = -1;
idx = 0;
M = cin.nextInt();
for(int i= 0; i<M; i++){
String F = cin.nextStr();
if(F.equals("H")){ int x = cin.nextInt(); in_to_head(x);}
if(F.equals("D")){ int k = cin.nextInt();
if(k == 0){ head = en[head]; }
else{ remove(k-1);}
}
if(F.equals("I")){ int z = cin.nextInt(); int c = cin.nextInt(); add(z-1, c); }
}
for(int i = head; i!=-1; i = en[i] ){
cout.printf("%d ",e[i]);}
}catch(Exception e){
}finally{
cout.close();
}
}
static void in_to_head(int x){
e[idx] = x;
en[idx] = head;
head = idx;
idx++;//为下一次做准备
}
static void add(int k,int x){
e[idx] = x;
en[idx] = en[k];
en[k] = idx; //被插入的元素的下标 = 当前“第idx个”元素(即;当前最新插入元素的下标)
idx++;//为下一次做准备
}
static void remove(int k){
en[k] = en[en[k]];
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【KMP】(2023.2.24)
import java.io.*;
import java.util.*;
public class Main{
private static PrintWriter cout = new PrintWriter(System.out);
static reader cin =new reader();
static int N,M;
static char p[] = new char[100000+10];
static char s[] = new char[1000000+10];
static int ne[] = new int[100000+10];
public static void main(String arg[]){
try{
String temp;
N = cin.nextInt();
temp = cin.nextStr();
p = temp.toCharArray();
M = cin.nextInt();
temp = cin.nextStr();
s = temp.toCharArray();
sol();
// kmp start !
for (int i = 0, j = -1; i < M; i ++)
{
while (j != -1 && s[i] != p[j + 1])
{
j = ne[j];
}
if (s[i] == p[j + 1])
{
j ++; // 匹配成功时,模板串指向下一位
}
if (j == N - 1) // 模板串匹配完成,第一个匹配字符下标为 0,故到 n - 1
{
// 匹配成功时,文本串结束位置减去模式串长度即为起始位置
cout.printf("%d ",i-j);
// 模板串在模式串中出现的位置可能是重叠的
// 需要让 j 回退到一定位置,再让 i 加 1 继续进行比较
// 回退到 ne[j] 可以保证 j 最大,即已经成功匹配的部分最长
j = ne[j];
}
}
}catch(Exception e){
}finally{
cout.close();
}
}
//查找所有的next[];
static void sol(){
ne[0]= -1;
for(int i=1, j =-1; i<N; i++ ){
while( j!=-1 && p[i]!=p[j+1] ){
j = ne[j];
}
if(p[i]==p[j+1]){
j++;
}
ne[i] = j;
}
}
}
class reader{
StringTokenizer st;
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【简易树存储并查找字符集合】(2023.2.25)
本题利用了树结构的特点来记录自己维护的字符串集合中有哪些字符串,重点是利用两个数组分别来记录 某一结点是否存在字符(二维数组son[N] [26])、某结点是否是字符串的结尾并且有多少个(即有多少个字符串)(一维数组cnt[N])
另外一个要点就是:利用Ascii码的特性:
某一个小写字母 - 'a' = 该字母在字母表中的顺序位
如:'b' - 'a' = 1
import java.util.*;
import java.io.*;
public class Main{
static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int N = 100000+10;
static int son[][]=new int[N][26];//Trie树中每个节点的所有儿子
static int cnt[]=new int[N];//以当前这个点结尾的单词有多少个
static int idx;
public static void main(String arg[]){
try{
int n = cin.nextInt();
while(n-- >0){
String f = cin.nextStr();
if(f.equals("I")){
String temp = cin.nextStr();
insert(temp.toCharArray());
}
if(f.equals("Q")){
String temp = cin.nextStr();
cout.println(view(temp.toCharArray()));
}
}
}catch(Exception e){
}finally{
cout.close();
}
}
static void insert(char []str){
int size = str.length;
int p = 0;
for(int i=0; i<size; i++){
int u = str[i]-'a';//编号
//son[p][u]存储的在哪一个节点上,二维空间指的是该字母是否在树的当前结点出现
if(son[p][u]==0){ son[p][u]=++idx; }
p = son[p][u];//到下一个结点处,且p代表的是此时所处的树的深度
}
cnt[p]++;//以此深度结尾的单词数+1
}
static int view(char []str){
int p = 0;
for(int i= 0; i<str.length; i++){
int u = str[i]-'a';
if(son[p][u]==0){ return 0; }
p = son[p][u];
}
return cnt[p];
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while( st==null || !st.hasMoreTokens() ){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【分数化简(找规律)】(2023.2.26)
重点是解析进行分子分母同时变化的过程并进行模拟
class Solution {
public int[] fraction(int[] cont) {
int fenmu = cont[cont.length-1];
int fenzi = 1;
for(int i=cont.length-2; i>=0; i--){
int temp = fenmu;
fenmu = cont[i]*fenmu+fenzi;
fenzi = temp;
if(fenzi % fenmu == 0){
fenzi = fenzi/fenmu;
fenmu = 1;
}
}
return new int []{fenmu,fenzi};
}
}题记【余数特征(找规律)】(2023.2.27)
6368. 找出字符串的可整除数组 - 力扣(Leetcode)
利用余数的性质:某一个数的前n位数关于m的余数,只与其最后一位的上一位关于m的余数有关,具体关系表达式如下:
char str[] ; //代表目标数串,如:143556
r = ( r * 10 + str[i] - '0' ) % m
//即针对上面的目标串143556: 第一二位构成的数14 的 关于m的余数 只与第二位4的上一位1的余数有关,比如: 此时取m为2,r%2=1,则:
//即:r(4) = ( r(1)*10 + 4 ) % 2 = 0
其他的前n位数(前缀数)也同理
class Solution {
public int[] divisibilityArray(String word, int m) {
int len = word.length();
char str[] = new char[len];
int in[] = new int[len];
long r =0;
str = word.toCharArray();
for(int i =0; i<len; i++){
r = (r*10 + str[i] - '0') % m;
if (0 == r) in[i] = 1;
else in[i] = 0;
}
return in;
}
}题记【有效类型匹配(二叉树前序遍历)】(2023.2.27)
主要注意在前序遍历的过程中如何对需要的形式(< , >)进行构造
还有就是要注意抓住特征及匹配的条件
import java.util.*;
import java.io.*;
public class Main{
private static PrintWriter cout= new PrintWriter(System.out);
static reader cin = new reader();
static int n;
static String str[];
static StringBuffer ans = new StringBuffer();
static int index;
public static void main(String arg[]){
try{
index = 0;
n = cin.nextInt();
str = cin.nextLine().split(" ");
if(dfs() && index==str.length-1 ){ cout.println( ans.toString() );}
else{ cout.println("Error occurred"); }
}catch(Exception e){
}finally{
cout.close();
}
}
static boolean dfs(){
if(index< str.length){
if(str[index].equals("pair")){
ans.append("pair");
}else{
ans.append("int");
}
if(str[index].equals("pair")){
ans.append("<");
index++;
if(!dfs()){ return false; }
ans.append(",");
index++;
if(!dfs()){ return false; }
ans.append(">");
}
return true;}
else{
return false;
}
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st==null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
String nextLine(){
try{
return br.readLine();
}catch(Exception e){
}
return "";
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【(LIS)最长上升子序列】(2022.3.5)
此题的数据范围决定了是否能够采取暴力的手段进行解题:
当1≤N≤1000时就可以用朴素做法
当1≤N≤100000时朴素算法就会超时,因为朴素做法的时间复杂度此时会很高
朴素做法:(纯dp)
相当于只是进行了筛除没必要的数据搜索,但是总体的时间复杂度还是很高
此处的dp[ ]数组相当于就是f(c),而最终的最长上升子序列长度实际上就是f(x),
所以求出所有的f(c)后,再每次更新f(x)【即最大上升子序列的长度】即可
import java.io.*;
import java.util.*;
public class Main{
static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int n;
static int a[];
static int dp[];
//static int tail[] = new int[100010];
public static void main(String args[]){
try{
n = cin.nextInt();
a = new int[n];
dp = new int[n];
for(int i = 0; i<n; i++ ){
a[i] = cin.nextInt();
}
//必须先将dp所有元素置为1
Arrays.fill(dp,1);
int len = 0;
for(int i=0; i<n; i++){
for(int j=0; j<i; j++){
//如果满足递增的条件就用 大于当前dp[i]的值(即dp【j】的值)+1 来更新当前dp[i]【代表递增长度加1】
//以下内容也表示了
if(a[j]<a[i]){ dp[i] = Math.max(dp[i], dp[j]+1); }
}
len = Math.max(len,dp[i]);
}
cout.printf("%d",len);
cout.printf("最大上升子序列:" );
for(int i = 0; i<n; i++ ){
cout.printf("%d ", dp[i] );
}
}catch(Exception e){
}finally{
cout.close();
}
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st == null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}二分【查找】+贪心【做出局部最优解】
此时:tail数组的下标就代表的是长度,其tail数组的值代表当前长度中的最新的最小值是多少(eg:tail[3]=2,代表长度为4时,表示当前的最新的最小值为2)
import java.io.*;
import java.util.*;
public class Main{
static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int n;
static int a[];
static int tail[];
//static int tail[] = new int[100010];
public static void main(String args[]){
try{
n = cin.nextInt();
a = new int[n];
tail = new int[n];
for(int i = 0; i<n; i++ ){
a[i] = cin.nextInt();
}
cout.printf("%d",lengthOfLIS(a));
}catch(Exception e){
}finally{
cout.close();
}
}
static int lengthOfLIS(int[] nums) {
int len = 0;
for(int i=0; i<n; i++){
int l = 0, r= len;
while(l<r){
int mid = (l+r)>>1;
if(tail[mid]<nums[i]){ l = mid+1; }
else{ r = mid; }
}
tail[l] = nums[i];
if(l==len){ len++; }
}
return len;}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st == null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【(LIS)双向最长上升子序列】(2023.3.6)
我们知道,一个序列的子序列,就是通过删去原序列中部分的元素后构成的
因此,找到满足该类型序列,最少需要删除的元素数量 就等价于 "找到满足该类型序列,最长子序列的长度"
对于案例:
8
186 186 150 200 160 130 197 220最少需要 4 名同学出列:186 150 197 220
在这个地方:f_up[ ],f_dw[ ] 分别指:在遍历时到某个i时【上升(下降)】最多有多少个同学构成【上升(下降)】的关系。
import java.io.*;
import java.util.*;
public class test{
static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static final int N = 110;
static int n;
static int a[] = new int[N];
static int f_up[]=new int [N];
static int f_dw[]=new int [N];
public static void main(String args[]){
try{
n = cin.nextInt();
for(int i = 1; i<=n; i++ ){
a[i] = cin.nextInt();
}
a[0] =0;
for(int i=1; i<=n; i++){
for(int j=0; j<i; j++){
if(a[i]>a[j]){ f_up[i] = Math.max(f_up[i], f_up[j]+1); }
}
}
cout.printf("最大上升子序列:\n" );
for(int i = 0; i<n; i++ ){
cout.printf("%d ", f_up[i] );
}
cout.printf("\n");
a[n+1] =0;
for(int i=n; i>0; i--){
for(int j=n+1; j>i; j--){
if(a[i]>a[j]){ f_dw[i] = Math.max(f_dw[i], f_dw[j]+1); }
}
}
cout.printf("最大下降子序列:\n" );
for(int i = 0; i<n; i++ ){
cout.printf("%d ", f_dw[i] );
}
cout.printf("\n");
int res = 0;
for (int i = 1; i <= n; ++ i) res = Math.max(res, f_up[i] + f_dw[i] - 1);
cout.printf("最少需要 %d 名同学出列\n",n-res);
}catch(Exception e){
cout.println(e.getMessage());
}finally{
cout.close();
}
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st == null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【(LCS)最长公共子序列】(2023.3.6)
题记【(贪心)数塔问题】(2023.3.6)
本质上就是一道经典的dp【动态规划】问题
可以尝试两种做法:从上面开始dp和从下面开始dp
从下面开始(常规思路):
把每个位置找到上一个位置的最大值并和自己的值相加,然后将这个和记录到自己的名下,然后在找最终路径的时候找第一个数的值即可,即此处:整体的问题是求出最短路径f(x),局部的小问题f(c)是求两层之间的最大值之和并将此值存储下来方便解决下一个 需要用到该局部小问题的解的 局部问题
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();//表示总共有多少行
//数塔用斜三角表示
int a[][]=new int[n][n];
//构造数塔
for(int i=0;i<n;i++){
for (int j=0;j<=i;j++) {
a[i][j] = sc.nextInt();
}
}
//打印一下数塔,看是否正确
for (int[] ints : a) {
System.out.println(Arrays.toString(ints));
}
//找出最大值路径
for(int i=n-2;i>=0;i--){
for(int j=0;j<=i;j++) {
a[i][j]=a[i][j]+Math.max( a[i+1][j], a[i+1][j+1] );
}
}
System.out.println(a[0][0]);
}
}从上面开始找:
整体思路和上面一样,但是将最终解max【即f(x)】进行实时更新(在往下寻找每一个局部最优解【即f(c)】之后进行更新),最终达到找到整体最优解的目的
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int a[][] = new int[n+1][n+1];
int max = 0;
for(int i=1; i<=n; i++){
for(int j =1; j<=i; j++){
a[i][j]= scan.nextInt();
a[i][j] = Math.max( a[i][j]+a[i-1][j],a[i-1][j-1]+a[i][j] );
max = Math.max( max,a[i][j] );
}
}
System.out.println(max);
scan.close();
}
}题记【数论知识】(2023.3.17)
蓝桥杯 2017 省 B] k 倍区间(前缀和枚举/数论优化)
import java.util.*;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
private static PrintWriter cout= new PrintWriter(System.out);
static reader cin = new reader();
static final int N = 100010;
static int a[]= new int[N];
static int b[]= new int[N];
static int n,k;
public static void main(String[] args) {
try{
n = cin.nextInt();
k = cin.nextInt();
long sum = 0;
int t = 0;
for(int i=1; i<=n; i++){
t = cin.nextInt();
a[i] = (a[i-1]+t)%k;
sum += b[a[i]]++;
}
sum += b[0];
cout.printf("%d",sum);
}catch(Exception e){
}finally{
cout.close();
}
}
}
class reader{
StringTokenizer st;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st==null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【Stringbuilder运用】(2023.3.17)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
StringBuilder A = new StringBuilder(scan.nextLine());
StringBuilder B = new StringBuilder(scan.nextLine());
StringBuilder card = new StringBuilder();
int count = 1;
while (A.length() != 0 && B.length() != 0) {
StringBuilder temp = new StringBuilder();
if (count % 2 != 0) {
for (int i = card.length() - 1; i >= 0; i--) {
if (A.charAt(0) == card.charAt(i)) {
A.append(A.charAt(0));
A = new StringBuilder(A.substring(1));
temp = new StringBuilder(card.substring(i));
card = new StringBuilder(card.substring(0, i));
A.append(temp.reverse());
}
}
card.append(A.charAt(0));
//更新A的值
A = new StringBuilder(A.substring(1));
} else {
for (int i = card.length() - 1; i >= 0; i--) {
if (B.charAt(0) == card.charAt(i)) {
B.append(B.charAt(0));
B = new StringBuilder(B.substring(1));
temp = new StringBuilder(card.substring(i));
card = new StringBuilder(card.substring(0, i));
B.append(temp.reverse());
}
}
card.append(B.charAt(0));
B = new StringBuilder(B.substring(1));
}
count++;
}
System.out.println(A.append(B));
}
}题记【text类中格式指定SimpleDateFormat对象的使用】(2023.3.17)
import java.util.Scanner;
import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Date;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
private static Scanner in;//静态域
public static void main(String[] args) throws ParseException {
in = new Scanner(System.in);
int T=in.nextInt();
in.nextLine();//去除换行符
for(int i=0;i<T;i++) {
long time1=getTime();
long time2=getTime();
long t=(time1+time2)/2;
System.out.printf("%02d:%02d:%02d\n",t/3600,t/60%60,t%60);
}
}
//返回当前两个时间的秒数差值
private static long getTime() throws ParseException {
String line = in.nextLine();
String[] split = line.split(" ");//以空格为分隔符
//时间解析的API SimpleDateFormat
SimpleDateFormat format = new SimpleDateFormat("HH:mm:ss");
//format.parse(split[0])解析字符串为日期
Date t1 = format.parse(split[0]);
Date t2 = format.parse(split[1]);
int d = 0;
if(split.length == 3){
//(+1) split[2].substring(2,3) 字符串获取1,用Integer解析转换为int
d = Integer.parseInt(split[2].substring(2,3));
}
//返回秒数
return d*24*3600+t2.getTime()/1000-t1.getTime()/1000;//getTime()得到时间代表的毫秒数,故需要除以1000才表示秒数
}
}题记【较大质数】(2023.3.29)
import java.util.*;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
static int n;
static int ma;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
//在此输入您的代码...
n = scan.nextInt();
int i,j =0;
for(i=2; i<=Math.sqrt(n); i++){
if(n%i==0){
j=n/i;
break;
}
}
if(i>j){
ma= i;
}
else{
ma= j;
}
System.out.println(ma);
scan.close();
}
}题记【质数拆分】(2023.3.31)
本质上就是要你 “分解质因数” ,但是由于是求总体方案数,所以才会想到是使用动态规划(dp)
使用01背包模型(动态规划):
动态规划解题步骤主要分两步:
①找出dp[i] [j]的含义
②依据题意找出状态转移方程
dp[i] [j]的含义是前 i 个质数刚好组成 j 有几种方法
寻找 状态转移方程 :
在统计dp[i] [j]时如果 j<arr[ i ]: 那么就说明 j 无法分解为arr[i]和另一个质数的和,那么dp[i] [j]=dp[i-1] [j],因为前i个质数肯定包含了前i-1个质数。
相反如果 j>=arr[i]: 则dp[i] [j]除了等于dp[i-1] [j]外还要加上dp[i-1] [ j-arr[i] ],因为如果质数可以组成j-arr[i]则加上arr[i]也可以组成j。
import java.util.*;
import java.io.*;
public class test{
static PrintWriter cout = new PrintWriter(System.out);
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//dp[i] [j] 表示:对前 i 个质数中的和 刚好是 j 的方案数
static long dp[][] = new long[2020][2020];
static int a[] = new int[2020];
public static void main(String[] args) {
try{
int k=1;
for(int i=2; i<2019; i++){
if(jug(i)){
a[k++] = i;
}
}
dp[0][0] = 1;//起始方案数为1
for(int i=1; i<=k; i++){
for(int j=0; j<=2019; j++){
//如果容量不足,则将前i个质数组合的方案 数就等于将前i-1个质数组合的方案数
//【即:不选第i个质数a[i]】
if(j<a[i]){
dp[i][j] = dp[i-1][j];}
//如果此时容量足够的话,则此时的方案数就 加上 将前i-1个质数组合达到j-a[i]的方案 数(相当于统计进了第i个质数)
//【即:选第i个质数a[i]】
else{
dp[i][j] += dp[i-1][j-a[i]];
}
}
}
cout.println(dp[k-1][2019]);
}catch(Exception e){
cout.println(e.toString());
}finally {
cout.close();
}
}
//判断是否为质数
static boolean jug(int x){
for(int i=2; i<x; i++){
if(x%i==0) return false;
}
return true;
}
}题记【Arraylist类运用】(2023.4.1)
import java.util.*;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
static PrintWriter cout = new PrintWriter(System.out);
static reader cin = new reader();
static int n,m;
public static void main(String[] args) {
try{
n = cin.nextInt();
m = cin.nextInt();
ArrayList<Integer> a = new ArrayList<Integer>();
init(a);
print(a);
cout.println("");
while((m--)>0) {
String temp = cin.nextStr();
int ft = cin.nextInt();
int te = a.indexOf(ft);//3的下标为2
//cout.println(te);
if (temp.equals("L")) {
ArrayList<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < te; i++) {
l.add(a.get(i));
}
for (int i = 1; i <= te; i++) {
a.set(i, l.get(i - 1));
}
a.set(0, ft);
}
if (temp.equals("R")) {
ArrayList<Integer> r = new ArrayList<Integer>();
a.remove(te);
a.add(ft);
}
}
print(a);
}catch(Exception e){
cout.println(e.toString());
}finally{
cout.close();
}
}
static void init(ArrayList<Integer> x){
for(int i=1; i<n+1; i++){
x.add(i);
}
}
static void print(ArrayList x){
for(Object i: x){
cout.printf("%d ",i);
}
}
}
class reader{
StringTokenizer st;
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
String nextStr(){
try{
while(st==null || !st.hasMoreTokens()){
st = new StringTokenizer(br.readLine());
}
}catch(Exception e){
}
return st.nextToken();
}
int nextInt(){
return Integer.parseInt(nextStr());
}
}题记【sort排序以及数组模拟】(2023.4.2)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Comparator;
public class Main {
static int N = 100020;
static long ant [] = new long [N+1];
static long ans [] = new long [N+1];
public static void main(String agrs[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s [] = br.readLine().split(" ");
int n = Integer.parseInt(s[0]);
int d = Integer.parseInt(s[1]);
int k = Integer.parseInt(s[2]);
int bak=n;
int nums[][] = new int [n][2];
for(int i=0;i<n;i++) {
s = br.readLine().split(" ");
nums[i][0] = Integer.parseInt(s[0]);//时间
nums[i][1] = Integer.parseInt(s[1]);//编号
}
//按照时间来排序
Arrays.sort(nums,new Comparator<int []>() {
@Override
public int compare(int[] o1,int[] o2) {
// TODO Auto-generated method stub
return o1[0]-o2[0];
}
});
for(int i=0;i<n;i++) {
//id
int num = nums[i][1];
//时间
int num2 = nums[i][0];
if(ans[num]==0) {
//当前id下标对应的时间为num2
ant[num]=num2;
//当前id点赞数+1
ans[num]++;
}else if(Math.abs(num2-ant[num])<d) {//相差时间
ant[num]=num2;
ans[num]++;
}else {//超出了最大相差时间
if(ans[num]>=k)continue;
ant[num]=num2;//无论什么情况都要更新当前id下标下的时间为num2
ans[num]=1;//重置该id的点赞数
}
}
for(int i=0;i<=N;i++) {
if(ans[i]>=k) {
System.out.println(i);
}
}
// for(int i=0;i<n;i++) {
// System.out.println(Arrays.toString(nums[i]));
// }
}
}题记【分别分解质因数】(2023.4.6)
例如:90的公因子为2,3,5,9,10,15 ·········
我们要用90从小到大除以它的公因子(注意:一个公因子可以被除多次)
1.我们先用最小的公因子除90: 90/2=45;(这一步分解出因子2)
2.因为45不能被2整除,所以就用下一个公因子3: 45/3=15(这一步分解出因子3)
3.因为15能被当前公因子3整除,那么: 15/3=5;(这一步分解出因子3)
4.继续,因为5不能被3整除,那么:5/5=1(这一步分解除因子5) (这里最后一步的结束条件是得到的数 1 % 因数!= 0)
这里按照我们的顺序把90分成了2 3 3 * 5
求出区间[a,b]中所有整数的质因数分解。
public static void main(String[] args) {
try{
int a,b,n,i,j;
a = cin.nextInt();
b = cin.nextInt();
for(i=a; i<=b; i++){
cout.printf("%d=",i);
n=i;
j=2;
while(n!=j){ // 一直除到最后一个 也就是n==j
for(j=2; j<n; j++){
if(n%j==0 && n!=j){
cout.printf("%d*",j);
n/=j;
break;
}
}
}cout.printf("%d\n",n);
}//15 = 3*n
}catch(Exception e){
cout.println(e.toString());
}finally {
cout.close();
}
}题记【阶乘约数】(2023.4.6)
任意一个正整数x都可以表示成若干个质数乘积的形式
而拆分后的约数个数就是:(各个质因子的出现次数+1)连乘
正约数个数=(a1+1)*(a2+1)...(an+1),a1、a2、an分别是各个质因子的出现次数
eg:比如8=2 2 2(我们自己数一下可以知道约数为1,2,4,8) 即:正约数个数=(3+1)=4
public class Main {
public static int[] arr;
public static long sum=1;//开始就设定sum为1是因为提前指定:(0+1)【1不是质数】
public static void main(String[] args) {
arr = new int[101];
for (int i = 2; i <=100 ; i++) {
zhiyin(i);
}
for (int i = 2; i <=100; i++) {
if(arr[i]!=0){
sum*=(arr[i]+1);
}
}
System.out.println(sum);
}
//统计每个n的各个质因数出现的次数,并用arr数组记录下来(分别记录到质数下标的位置下)
public static void zhiyin(int n){
int i=2;
while(n!=1){
if(n%i==0&&isPrime(i)){
arr[i]++;
n/=i;
}else{
i++;
}
}
}
public static boolean isPrime(int x){
if(x==0||x==1){
return false;
}
for (int i = 2; i <=Math.sqrt(x) ; i++) {
if(x%i==0){
return false;
}
}
return true;
}
}题记【序列求和】(2023.4.7)
由 质因数分解定理 就可以进行一个模拟(排列组合)
import java.util.*;
public class Main {
static int testCount=60;//题目要求计算前60个
static int ii=100;//每个指数遍历的上限
static long result[]=new long[61];//用了存放前60个的答案
public static void main(String[] args) {
//a1-a4均从0开始模拟才能保证和中有pow(1,0)即1存在
for (int a4 = 0; a4 <= ii; a4++) {
for (int a3 = 0; a3 <= ii; a3++) {
for (int a2 = 0; a2 <= ii; a2++) {
for (int a1 = 0; a1 <= ii; a1++) {
int t=(a1+1)*(a2+1)*(a3+1)*(a4+1);//计算此种指数组合下的t为多少
if(t<=60) {//稍稍优化一下,大于60的题目不要求计算,优化掉
long single=(long) (Math.pow(2, a1)*Math.pow(3, a2)*Math.pow(5, a3)*Math.pow(7, a4));//计算此种指数组合下的n为多少
// System.out.println(a1+" "+a2+" "+a3+" "+a4+" "+t+" "+single);
if(single<result[t] || result[t]==0) {//n需要在所有含有t个约数的数中最小,所有计算结果比之前小才更新答案
result[t]=single;
}
}
}
}
}
}
long sum=0;
for (int i = 1; i <= testCount; i++) {
sum+=result[i];
}
System.out.println(sum);//最终答案
}
}题记【求一定范围内的质数】(2023.4.7)
使用了埃式筛法
其思路是:用已经筛选出来的素数去过滤所有能够被它整除的数。
public class test {
static PrintWriter cout = new PrintWriter(System.out);
public static final int inf =100002;
static final int N =10000000;
static boolean f[] = new boolean[N];
static long a[] = new long [N];
public static void main(String[] args) {
try{
int ind =0;
Arrays.fill(f,false);
for(int i =2; i< N; i++ ){
if(!f[i]){
a[ind++] =i;
for(int j= i+i; j<N; j+=i){
f[j] =true;
}
}
}
cout.println(a[100001]);
}catch(Exception e){
cout.println(e.toString());
}finally {
cout.close();
}
}
public static boolean isPrime(int x){
if(x==0||x==1){
return false;
}
for (int i = 2; i <=Math.sqrt(x) ; i++) {
if(x%i==0){
return false;
}
}
return true;
}
}题记【String操作及质数判断】(2023.4.7)
对于某些数字需要进行是否包含某个值的数字的判断,一定要多往字符串的应用上想,这样往往能够快速解决问题。
import java.io.*;
import java.util.*;
public class Main{
public static void main(String[] args) {
int count = 0 ;
for(int i = 2 ; i <= 20210605;i++) {
if((i>10) && (i%2==0||i%3==0||i%5==0||i%7==0) ) continue;
if(check(i) && isNum(i)) {
//System.out.println(i);
count++;
}
}
System.out.println(count);
}
static boolean check(int n ) {
for(int i = 2 ; i*i<=n;i++) {
if(n%i==0) return false;
}
return true;
}
static boolean isNum(int n ) {
String str = n + "";
String ff = "014689";
for(int i = 0 ; i <str.length();i++) {
if(ff.contains(str.charAt(i)+"")) return false;
}
return true;
}
}